DeepLearing学习笔记-改善深层神经网络(第二周作业-优化方法)_random_mini_batches(-程序员宅基地
技术标签: deep-learning 深度学习 神经网络
0- 背景:
本文将介绍几种常用的优化方法,用以加快神经网络的学习速度
本文需要用到的库如下:
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'1- 梯度下降法
梯度下降是每次处理完 m 个样本后对参数进行一次更新操作,也叫做Batch Gradient Descent。
对于L层模型,梯度下降法对于各层参数的更新:
L表示层数, α 是学习率。所有的这些参数都存在 parameters 字典中。注意,循环是从L1开始。
# GRADED FUNCTION: update_parameters_with_gd
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
Update parameters using one step of gradient descent
Arguments:
parameters -- python dictionary containing your parameters to be updated:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients to update each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- the learning rate, scalar.
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Update rule for each parameter
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads['dW' + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads['db' + str(l+1)]
### END CODE HERE ###
return parameters测试代码:
parameters, grads, learning_rate = update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))测试代码运行如下:
W1 = [[ 1.63535156 -0.62320365 -0.53718766]
[-1.07799357 0.85639907 -2.29470142]]
b1 = [[ 1.74604067]
[-0.75184921]]
W2 = [[ 0.32171798 -0.25467393 1.46902454]
[-2.05617317 -0.31554548 -0.3756023 ]
[ 1.1404819 -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257]
[ 0.02561572]
[ 0.57539477]]梯度下降的一种变体是随机梯度下降法Stochastic Gradient Descent (SGD)。这等同于mini-batch中每个mini-batch只有一个样本的梯度下降法。此时,梯度下降的更新法则就变成,每个样本都要计算一次,而不是此前的对整个样本集计算一次。
两者代码如下:
- (Batch) Gradient Descent:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost.
cost = compute_cost(a, Y)
# Backward propagation.
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
- Stochastic Gradient Descent:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost = compute_cost(a, Y[:,j])
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters.
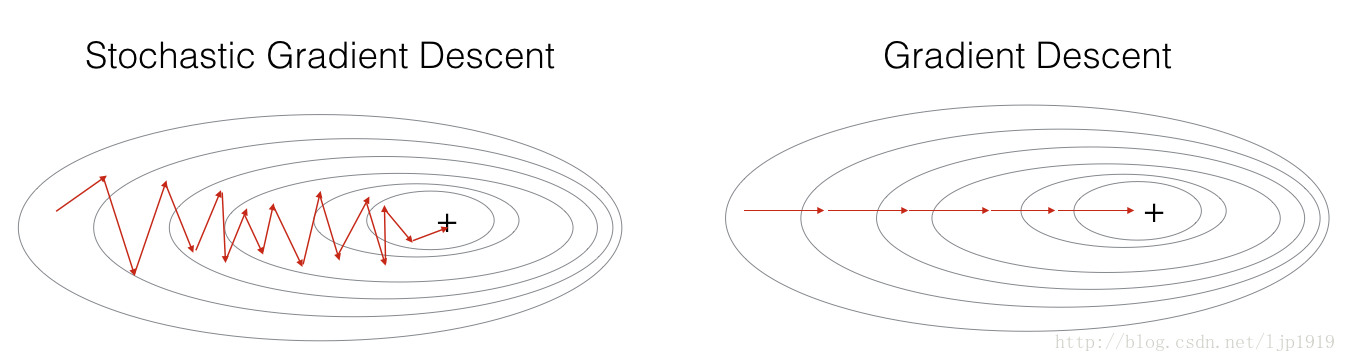
parameters = update_parameters(parameters, grads)在随机梯度下降中, 我们对于每个样本都更新梯度。当训练集很大时,这种方法可以明显提高运行速度,但是参数会沿着最小方向震荡,而不是平滑地收敛。
“+” 表示代价最小值。SGD在收敛前出现很多震荡,但是由于每步都只有一个样本,所以每步都比梯度下降GD要来得快。 (vs. the whole batch for GD).
注意 SGD 共需要三个循环:
1. 最外层的迭代次数
2. m 个训练样本
3. 每层参数的更新 (
在实际情况中,我们一般是折中,即所谓的 Mini-batch gradient descent。将整体的训练集分成子数据集,然后每个子训练集计算一次梯度下降。
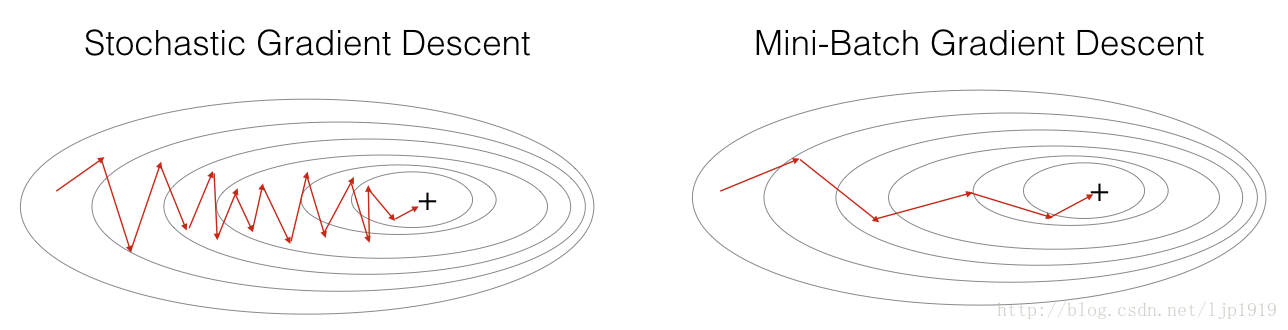
“+” 表示最小代价值。
谨记:
- gradient descent, mini-batch gradient descent 和 stochastic gradient descent之间的区别在于梯度更新所用到的样本数据量。
- 超参数学习率 α 是需要调整获取到
- mini-batch的尺寸也是调整获取到的,所以也是一个超参数。一般情况下这种方式比另外两者更好,特别是当训练集特别大的时候。
2 - Mini-Batch梯度下降
mini-batches用于训练集 (X, Y),一般有以下两个步骤:
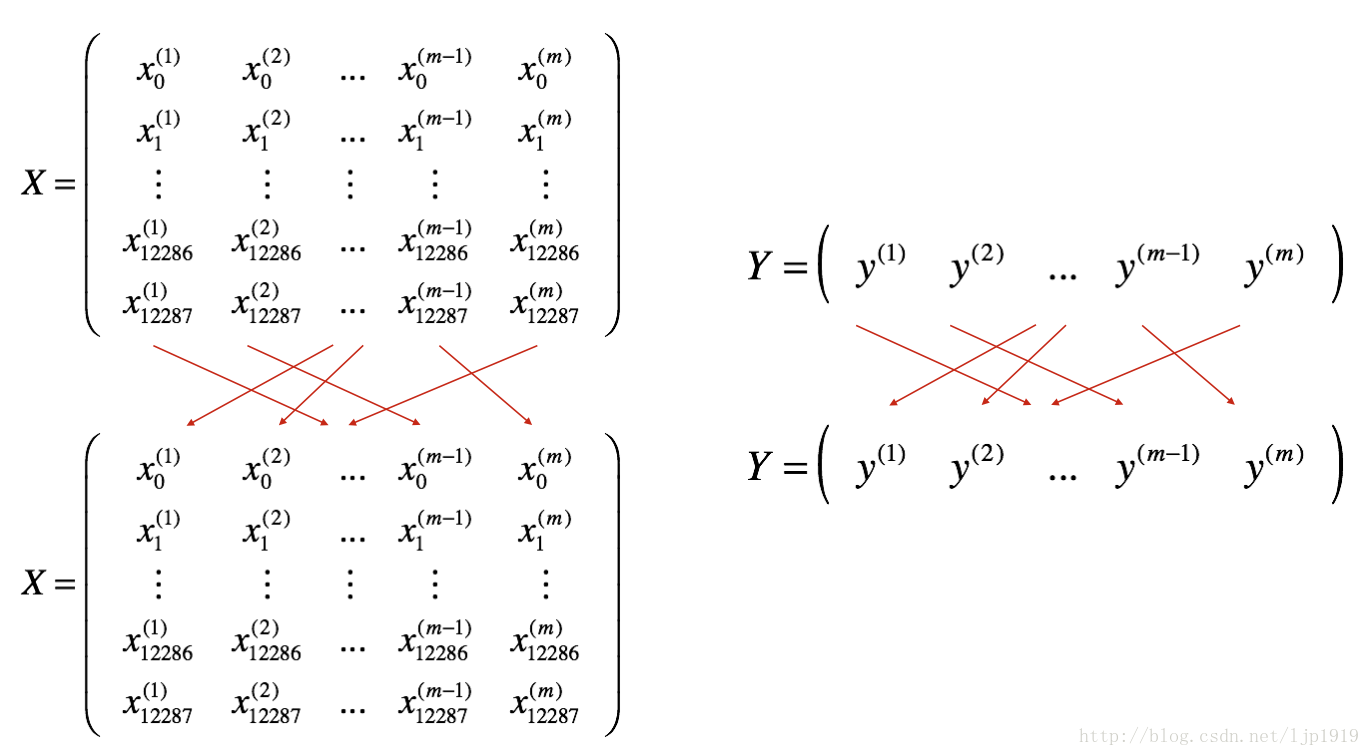
Shuffle(洗牌): 随机洗牌的方式将训练样本的数据顺序随机打散,注意:X和Y的随机要一致,否则Y值不能与X匹配,出现张冠李戴。随机化的洗牌操作能够将样本切分成不同的mini-batches。洗牌方式如下图所示:
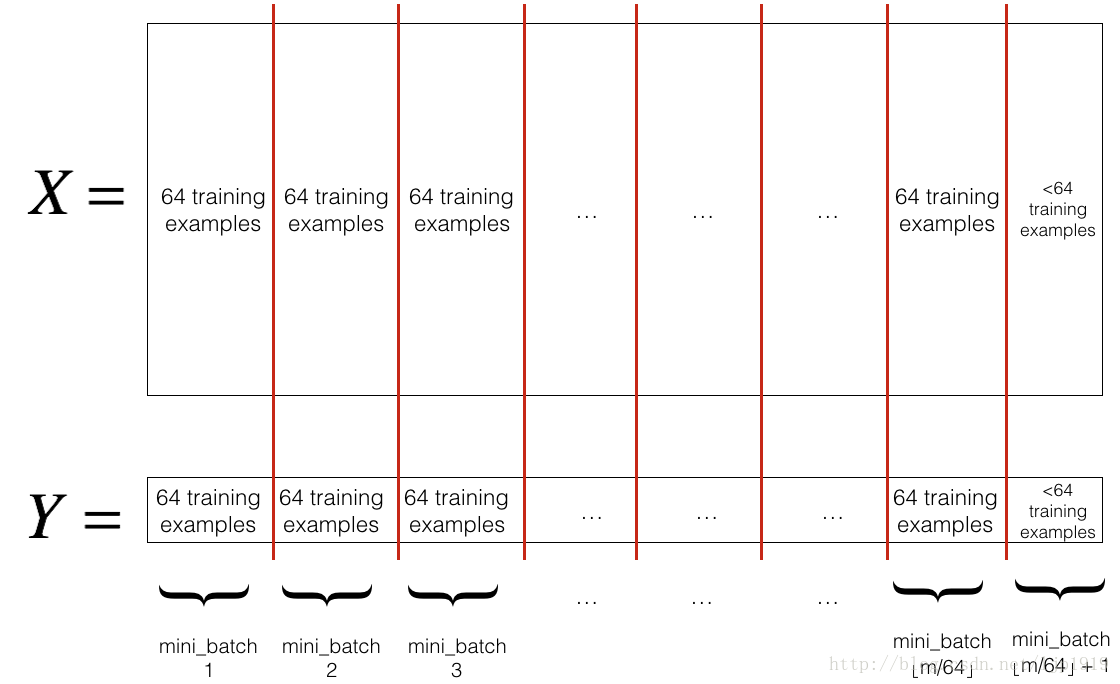
Partition(分割): 将已经随机化的数据集(X, Y)分割成
mini_batch_size(本文= 64)大小的子数据集。尾部的数据可能小于一个mini_batch_size,所以对于最后一个mini-batch要注意处理。
我们定义 random_mini_batches函数来实现上述功能。在采用索引切片的时候,操作 1st and 2nd mini-batches如下,其他依次。
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
...当样本数无法被mini_batch_size整除的时候,最后一个mini-batch< mini_batch_size=64。 ⌊s⌋ 表示 s 向下取整 (Python中实现:math.floor(s))。所以
代码实现如下:
# GRADED FUNCTION: random_mini_batches
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed) # To make your "random" minibatches the same as ours
m = X.shape[1] # number of training examples
#print("m=",m)
mini_batches = []
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
#print("num_complete_minibatches=",num_complete_minibatches)
for k in range(0, num_complete_minibatches):
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
#print(k)
# Handling the end case (last mini-batch < mini_batch_size)
# 尾数处理
#print(num_complete_minibatches * mini_batch_size)
if m % mini_batch_size != 0:
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : ]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : ]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches代码测试如下:
X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))测试代码运行输出结果如下:
shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]PS:一般mini-batch size的取值是 2n ,如 16, 32, 64, 128等
Momentum(动量梯度下降法)
由于min-batch梯度下降法是在看过训练集的一部分子数据集之后,就开始了参数的更新,那么就会在参数更新过程中出现偏差震荡。采用动量梯度下降法可以减缓震荡的出现。
momentum方式是在参数更新时候,参考历史的参数值,以平滑参数的更新。我们以变量 v 存储梯度变化的历史方向。一般情况下,这个
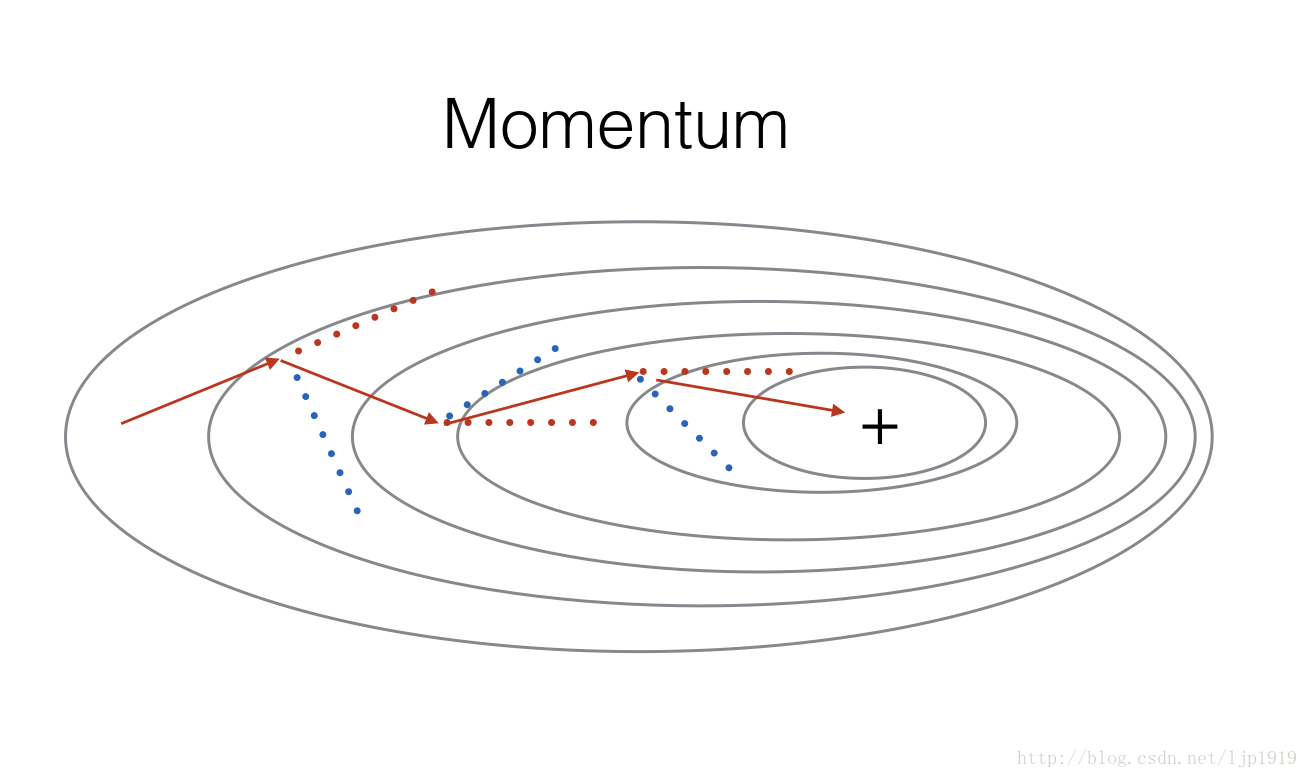
红色箭头表示在momentum作用下每个mini-batch梯度下降的方向,而蓝色则是没有momentum作用的mini-batch梯度下降方向。
velocity值初始化:
velocity,
grads 一致:
for l=1,...,L :
v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])initialize_velocity代码实现如下:
# GRADED FUNCTION: initialize_velocity
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
#print(parameters['W1'].shape)
# Initialize velocity
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
### END CODE HERE ###
return v初始化函数测试:
parameters = initialize_velocity_test_case()
v = initialize_velocity(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))测试结果如下:
v["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db1"] = [[ 0.]
[ 0.]]
v["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db2"] = [[ 0.]
[ 0.]
[ 0.]]带momentum的参数更新:
更新规则如下:
for l=1,...,L :
其中 L 表示层数, β 是momentum值, α 是学习率。 这些参数都存于 parameters 字典中。注意 W[1] and b[1] 是从第1层开始的。
update_parameters_with_momentum函数代码实现如下:
# GRADED FUNCTION: update_parameters_with_momentum
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Momentum update for each parameter
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
# compute velocities
v["dW" + str(l+1)] = beta * v["dW" + str(l+1)] + (1-beta) * grads['dW' + str(l+1)]
v["db" + str(l+1)] = beta * v["db" + str(l+1)] + (1-beta) * grads['db' + str(l+1)]
# update parameters
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]
### END CODE HERE ###
return parameters, v函数测试代码:
parameters, grads, v = update_parameters_with_momentum_test_case()
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))测试结果如下:
W1 = [[ 1.62544598 -0.61290114 -0.52907334]
[-1.07347112 0.86450677 -2.30085497]]
b1 = [[ 1.74493465]
[-0.76027113]]
W2 = [[ 0.31930698 -0.24990073 1.4627996 ]
[-2.05974396 -0.32173003 -0.38320915]
[ 1.13444069 -1.0998786 -0.1713109 ]]
b2 = [[-0.87809283]
[ 0.04055394]
[ 0.58207317]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[ 0.02344157]
[ 0.16598022]
[ 0.07420442]]注意 :
- velocity初始化为zeros,所以算法需要迭代一定次数以建立起速度,实现每次迭代的bigger steps。
- 当 β=0 ,则退化成标准的梯度下降法。
β 值得选取:
- β 越大,历史梯度值引入到当前值的权重越大,更新就会越平滑。但是如果 β 太大,则会导致更新平滑过度。
- β 一般取值在0.8 到 0.999之间,常取 β=0.9 。
- 可以通过尝试几个 β 值,然后看哪个值在降低cost function J 效果最好,来获取最优值。
4 - Adam算法
Adam算法应该是目前在神经网络领域最有效的优化算法了,该算法联合了RMSProp算法和Momentum算法。
Adam算法流程:
1.先计算历史梯度的指数加权平均值,存于变量
2. 计算历史梯度平方值的指数加权平均值,存于变量 s ,
3. 联合”1” and “2”更新参数
更新规则如下, for l=1,...,L :
其中:
- t 表示迭代的次数
- L 表示层数
- β1 and β2 都是超参数,控制指数加权的权重
- α 是学习率
- ε 是一个很小的值,为了避免除0操作
变量 v,s 的初始化如下:
for l=1,...,L :
v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
s["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
s["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
Adam的初始化代码:
# GRADED FUNCTION: initialize_adam
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
s["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
s["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
### END CODE HERE ###
return v, s代码测试:
parameters = initialize_adam_test_case()
v, s = initialize_adam(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))
测试代码输出:
v["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db1"] = [[ 0.]
[ 0.]]
v["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db2"] = [[ 0.]
[ 0.]
[ 0.]]
s["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
s["db1"] = [[ 0.]
[ 0.]]
s["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
s["db2"] = [[ 0.]
[ 0.]
[ 0.]]Adam算法实现:
# GRADED FUNCTION: update_parameters_with_adam
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for l in range(L):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1-beta1) * grads['dW' + str(l+1)]
v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1) * grads['db' + str(l+1)]
### END CODE HERE ###
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
### START CODE HERE ### (approx. 2 lines)
v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/(1-np.power(beta1,t))
v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-np.power(beta1,t))
### END CODE HERE ###
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
### START CODE HERE ### (approx. 2 lines)
s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1-beta2) * np.power(grads['dW' + str(l+1)],2)
s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1-beta2) * np.power(grads['db' + str(l+1)],2)
### END CODE HERE ###
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
### START CODE HERE ### (approx. 2 lines)
s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-np.power(beta2,t))
s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-np.power(beta2,t))
### END CODE HERE ###
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)
### END CODE HERE ###
return parameters, v, sAdam算法测试:
parameters, grads, v, s = update_parameters_with_adam_test_case()
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t = 2)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))测试代码运行如下:
W1 = [[ 1.63178673 -0.61919778 -0.53561312]
[-1.08040999 0.85796626 -2.29409733]]
b1 = [[ 1.75225313]
[-0.75376553]]
W2 = [[ 0.32648046 -0.25681174 1.46954931]
[-2.05269934 -0.31497584 -0.37661299]
[ 1.14121081 -1.09244991 -0.16498684]]
b2 = [[-0.88529979]
[ 0.03477238]
[ 0.57537385]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[ 0.02344157]
[ 0.16598022]
[ 0.07420442]]
s["dW1"] = [[ 0.00121136 0.00131039 0.00081287]
[ 0.0002525 0.00081154 0.00046748]]
s["db1"] = [[ 1.51020075e-05]
[ 8.75664434e-04]]
s["dW2"] = [[ 7.17640232e-05 2.81276921e-04 4.78394595e-04]
[ 1.57413361e-04 4.72206320e-04 7.14372576e-04]
[ 4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[ 5.49507194e-05]
[ 2.75494327e-03]
[ 5.50629536e-04]]5 - Model with different optimization algorithms
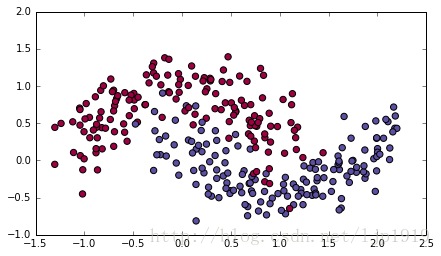
对于上述几种优化算法的测试,在这里我们采用 “moons” 数据集。
数据加载:
train_X, train_Y = load_dataset()对于一个3层的神经网络,我们将采用下述三种优化算法来训练:
- Mini-batch Gradient Descent: 通过调用:
update_parameters_with_gd()来实现
- Mini-batch Momentum: 通过调用:
initialize_velocity()和update_parameters_with_momentum()来实现。
- Mini-batch Adam: 通过调用:
initialize_adam()和update_parameters_with_adam()来实现
模型代码:
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
# Initialize parameters
parameters = initialize_parameters(layers_dims)
# Initialize the optimizer
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# Optimization loop
for i in range(num_epochs):
# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Forward propagation
a3, caches = forward_propagation(minibatch_X, parameters)
# Compute cost
cost = compute_cost(a3, minibatch_Y)
# Backward propagation
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# Update parameters
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
# Print the cost every 1000 epoch
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
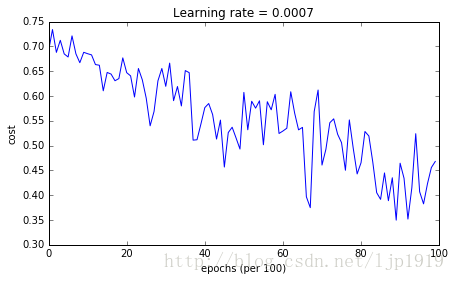
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters5-1 Mini-batch Gradient descent
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
Cost after epoch 0: 0.690736
Cost after epoch 1000: 0.685273
Cost after epoch 2000: 0.647072
Cost after epoch 3000: 0.619525
Cost after epoch 4000: 0.576584
Cost after epoch 5000: 0.607243
Cost after epoch 6000: 0.529403
Cost after epoch 7000: 0.460768
Cost after epoch 8000: 0.465586
Cost after epoch 9000: 0.464518Accuracy: 0.796666666667
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-2 Mini-batch gradient descent with momentum
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
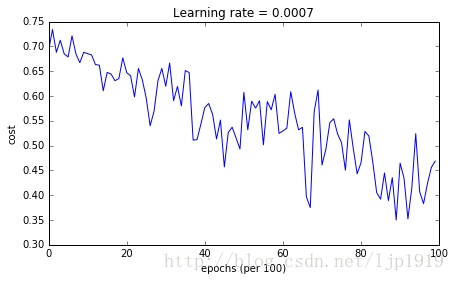
Cost after epoch 0: 0.690741
Cost after epoch 1000: 0.685341
Cost after epoch 2000: 0.647145
Cost after epoch 3000: 0.619594
Cost after epoch 4000: 0.576665
Cost after epoch 5000: 0.607324
Cost after epoch 6000: 0.529476
Cost after epoch 7000: 0.460936
Cost after epoch 8000: 0.465780
Cost after epoch 9000: 0.464740Accuracy: 0.796666666667
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-3 Mini-batch with Adam mode
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
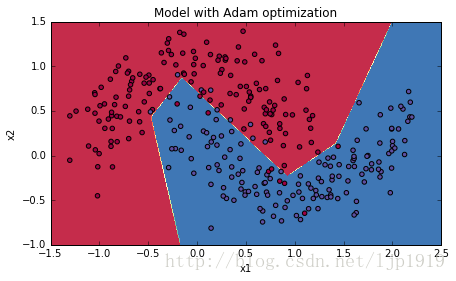
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
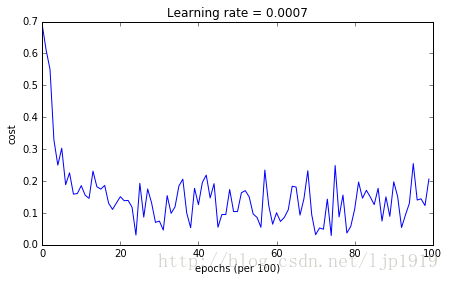
Cost after epoch 0: 0.690552
Cost after epoch 1000: 0.185567
Cost after epoch 2000: 0.150852
Cost after epoch 3000: 0.074454
Cost after epoch 4000: 0.125936
Cost after epoch 5000: 0.104235
Cost after epoch 6000: 0.100552
Cost after epoch 7000: 0.031601
Cost after epoch 8000: 0.111709
Cost after epoch 9000: 0.197648Accuracy: 0.94
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-4 总结:
| optimization method | accuracy | cost shape |
| Gradient descent | 79.7% | oscillations |
| Momentum | 79.7% | oscillations |
| Adam | 94% | smoother |
Momentum一般都是有助于提升速度,但是当学习率较小,数据集相对简单的时候,其性能的优越性没有太明显。我们在优化算法中看到的那些较大的震荡是由于一些minibatches 相对更加复杂所造成的。
从运行结果可以看出,Adam算法比mini-batch gradient descent 和 Momentum都要显得优越。对于model如果在简单数据集上,迭代次数更多的话,这三种优化算法都会产生较好的结果,但是我们也可以看出,Adam算法收敛得更快些。
Adam算法的优点:
- 内存要求低 (尽管比gradient descent 和 gradient descent with momentum要高些)
- 一般微调超参数就可以获得较好的结果(除了 α )
智能推荐
Ansible自动化运维工具主机清单配置
Ansible 提供了多种方式来定义和管理主机列表,除了默认的文件之外,您还可以使用自定义主机列表。这提供了更大的灵活性,允许您根据需要从不同来源获取主机信息。
堆栈的实现(C语言)_c语言堆栈-程序员宅基地
文章浏览阅读1.8k次,点赞6次,收藏36次。堆栈(stack)的基本概念堆栈是一种特殊的线性表,堆栈的数据元素及数据元素之间的逻辑关系和线性表完全相同,其差别是:线性表允许在任意位置插入和删除数据元素操作,而堆栈只允许在固定一端进行插入和删除数据元素操作。 堆栈中允许进行插入和删除数据元素操作的一端称为栈顶,另一端称为栈底。栈顶的当前位置是动态的,用于标记栈顶当前位置的变量称为栈顶指示器(或栈顶指针)。 堆栈的插入操作通常称为进栈或入栈,每次进栈的数据元素都放在原当前栈顶元素之前而成为新的栈顶元素。堆栈的删除操作通常称为出栈或退栈,每次出栈的_c语言堆栈
如何过滤敏感词免费文本敏感词检测接口API_违规关键词过滤api-程序员宅基地
文章浏览阅读1.6k次。敏感词过滤是随着互联网社区发展一起发展起来的一种阻止网络犯罪和网络暴力的技术手段,通过对可能存在犯罪或网络暴力可能的关键词进行有针对性的筛查和屏蔽,很多时候我们能够防患于未然,把后果严重的犯罪行为扼杀于萌芽之中。_违规关键词过滤api
ns3测吞吐量_ns3计算吞吐量-程序员宅基地
文章浏览阅读9.1k次,点赞2次,收藏42次。———————10月14日更—————————- 发现在goal-topo.cc中,由于Node#14被放在初始位置为0的地方,然后它会收到来自AP1和AP2的STA的OLSR消息(距离他们太近了吧)。 然而与goal-topo-trad.cc不同,goal-topo-trad.cc中Node#14可以在很远就跟自己的AP3通信,吞吐量比较稳定。而goal-topo.cc在开始的很长时间内并_ns3计算吞吐量
sqlite3中绑定bind函数用法 (将变量插入到字段中)_sqlite3_bind_double-程序员宅基地
文章浏览阅读7k次,点赞2次,收藏4次。转载至:https://blog.csdn.net/xiaoaid01/article/details/17892579 参数绑定:和大多数关系型数据库一样,SQLite的SQL文本也支持变量绑定,以便减少SQL语句被动态解析的次数,从而提高数据查询和数据操作的效率。要完成该操作,我们需要使用SQLite提供的另外两个接口APIs,sqlite3_reset和sqlite3..._sqlite3_bind_double
NotePad++自定义SQL语法高亮(文末附资源文件地址)_notepad sql 高亮规则-程序员宅基地
文章浏览阅读1.9k次。1、最终效果2、导入主题3、设置主题4、导入语法高亮配置文件5、使用_notepad sql 高亮规则
随便推点
Idea 运行spring项目 出现的bug_idea spring代理对象出bug-程序员宅基地
文章浏览阅读220次。Idea 运行spring项目 出现的bugbug 1错误信息:Cannot start compilation: the output path is not specified for module “02_primary”.Specify the output path in the Project Structure dialog.解决办法:..._idea spring代理对象出bug
JavaFx基础学习【四】:UI控件的通用属性_javafx教程-ui控件-程序员宅基地
文章浏览阅读1k次,点赞2次,收藏6次。Node,就是节点,在整体结构中,就是黄色那一块,红色也算个人理解,在实际中,Node可以说是我们的UI页面上的每一个节点了,比如按钮、标签之类的控件,而这些控件,大多都是有一些通用属性的,以下简单介绍一下。_javafx教程-ui控件
【嵌入式Linux】03-Ubuntu-文件系统结构_嵌入式linux使用ubuntu文件系统-程序员宅基地
文章浏览阅读136次。此笔记由个人整理塞上苍鹰_fly课程来自:正点原子_手把手教你学Linux一、文件系统结构g根目录:Linux下“/”就是根目录!所有的目录都是由根目录衍生出来的。/bin存放二进制可执行文件,这些命令在单用户模式下也能够使用。可以被root和一般的账号使用。/bootUbuntu内核和启动文件,比如vmlinuz-xxx。gurb引导装载程序。/dev设备驱动文件/etc存放一些系统配置文件,比如用户账号和密码文件,各种服务的起始地址。._嵌入式linux使用ubuntu文件系统
Win10黑屏卡死原因分析--罕见的内核pushlock死锁问题-程序员宅基地
文章浏览阅读2.1k次。此问题已向微软公司反馈,仅供学习参考这是微软内核的一个Bug.发生在内核函数 MmEnumerateAddressSpaceAndReferenceImages 和 MiCreateEnclave之间,如果时机不当会造成这两个函数之间死锁,而且还是一个pushlock死锁问题,十分罕见,这也是导致系统开机黑屏,系统突然卡死的元凶之一。Win10被骂了很久了,这次真的被我遇上了,系统无缘无故卡死_win10黑屏卡死原因分析--罕见的内核pushlock死锁问题
ie不支持java_巧用批处理解决IE不支持javascript等问题(转)-程序员宅基地
文章浏览阅读112次。巧用批处理解决IE不支持javascript等问题rem=====批处理开始========regsvr32actxprxy.dllregsvr32shdocvw.dllRegsvr32URLMON.DLLRegsvr32actxprxy.dllRegsvr32shdocvw.dllregsvr32oleaut32.dllrundll32.exeadvpack.dll/DelNo..._ie不支持javasript批处理
【STM32】GPIO输入-程序员宅基地
文章浏览阅读1.2k次,点赞16次,收藏20次。红外接收管等)的电阻会随外界模拟量的变化而变化,通过与定值电阻分压即可得到模拟电压输出,再通过电压比较器进行二值化即可得到数字电压输出。按键抖动:由于按键内部使用的是机械式弹簧片来进行通断的,所以在按下和松手的瞬间会伴随有一连串的抖动。当按键按下时,PA0被下拉到GND,此时读取PAO口的电压就是低电平;第一张图,当K1按下,PA0被下拉到GND,此时读取PAO口的电压就是低电平;当K1松开,PA0被悬空,引脚的电压不确定,此时必须要求PA0是。按键:常见的输入设备,按下导通,松手断开。