旋转矩阵、欧拉角、四元数理论及其转换关系

---

author@jason_ql（lql0716）
http://blog.csdn.net/lql0716

---

1、概述

旋转矩阵、欧拉角、四元数主要用于表示坐标系中的旋转关系，它们之间的转换关系可以减小一些算法的复杂度。

本文主要介绍了旋转矩阵、欧拉角、四元数的基本理论及其之间的转换关系。

2、原理

2.1 旋转矩阵

• 对于两个三维点 $p_1(x_1, y_1, z_1)$，$p_2(x_2, y_2, z_2)$，由点 $p_1$ 经过旋转矩阵 $R$ 旋转到 $p_2$，则有：

$$R = \left[ \begin{matrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{matrix} \right]$$

$$\left[ \begin{matrix} x_2 \\ y_2 \\ z_2 \end{matrix} \right] = R \left[ \begin{matrix} x_1 \\ y_1 \\ z_1 \end{matrix} \right]$$

注：旋转矩阵为正交矩阵$RR^T=E$

• 绕x轴旋转：

$$R_x(\theta) = \left[ \begin{matrix} 1 & 0 & 0\\ 0 & cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta \end{matrix} \right]$$

• 绕y轴旋转：

$$R_y(\theta) = \left[ \begin{matrix} cos\theta & 0 & sin\theta\\ 0 & 1 & 0\\ -sin\theta & 0 & cos\theta \end{matrix} \right]$$

• 绕z轴旋转：

$$R_z(\theta) = \left[ \begin{matrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0 & 1 \end{matrix} \right]$$

• 任意旋转矩阵：
  任何一个旋转可以表示为依次绕着三个旋转轴旋三个角度的组合。这三个角度称为欧拉角。
  三个轴可以指固定的世界坐标系轴，也可以指被旋转的物体坐标系的轴。三个旋转轴次序不同，会导致结果不同。

$$R_x(-\theta_1) R_y(-\theta_2) R_z(\theta) R_y(\theta_2) R_x(\theta_1)$$

2.2 欧拉角

• 欧拉角有两种：
  静态：即绕世界坐标系三个轴的旋转，由于物体旋转过程中坐标轴保持静止，所以称为静态。
  动态：即绕物体坐标系三个轴的旋转，由于物体旋转过程中坐标轴随着物体做相同的转动，所以称为动态。
  使用动态欧拉角会出现万向锁现象；静态欧拉角不存在万向锁的问题。

• 对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固定于刚体，随着刚体的旋转而旋转。

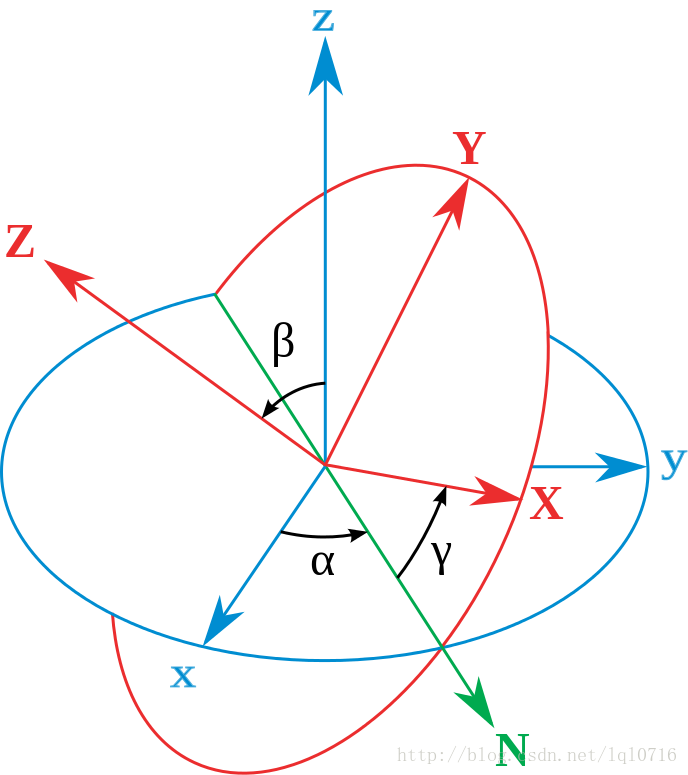
• 如图1，设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义：

  $\alpha$ 是x-轴与交点线的夹角，
  ${\displaystyle \beta }$ 是z-轴与Z-轴的夹角，
  ${\displaystyle \gamma }$ 是交点线与X-轴的夹角。

• 图1：
  
  图中三个欧拉角分别为：$(\alpha, \beta, \gamma)$；
  蓝色的轴为：$xyz轴$
  红色的轴为：$XYZ$轴
  绿色的线为交线：$N$
  $\alpha \in [0, 2\pi], \beta \in [0, \pi], \gamma \in [0, 2\pi]$

• 很可惜地，对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时，我们必须明确的表示出夹角的顺序，指定其参考轴。

• 实际上，有许多方法可以设定两个坐标系的相对取向。欧拉角方法只是其中的一种。此外，不同的作者会用不同组合的欧拉角来描述，或用不同的名字表示同样的欧拉角。因此，使用欧拉角前，必须先做好明确的定义。

• 欧拉角的基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。所以，欧拉旋转的三个角，可以对应于三个旋转矩阵。
  Yaw（偏航）：欧拉角向量的y轴
  Pitch（俯仰）：欧拉角向量的x轴
  Roll（翻滚）： 欧拉角向量的z轴

• Unity3D中，欧拉旋转是按照ZYX的顺序旋转的。（不同的旋转顺序最终得到的结果是不一样的，要引起重视。给定一组欧拉角角度值，比如yaw=45度，pitch=30度，roll=60度，按照yaw-pitch-roll的顺序旋转和按照yaw-roll-pitch的顺序旋转，最终刚体的朝向是不同的！换言之，若刚体需要按照两种不同的旋转顺序旋转到相同的朝向，所需要的欧拉角角度值则是不同的！）

• 欧拉角的缺点：

  1、 欧拉角的表示方式不唯一。给定某个起始朝向和目标朝向，即使给定yaw、pitch、roll的顺序，也可以通过不同的yaw/pitch/roll的角度组合来表示所需的旋转。这其实主要是由于万向锁(Gimbal Lock)引起的；

  2、欧拉角的插值比较难；

  3、计算旋转变换时，一般需要转换成旋转矩阵，这时候需要计算很多sin, cos，计算量较大；

2.2.1 由欧拉角求旋转矩阵

设三个轴x，y，z的欧拉角分别为$\theta_x, \theta_y, \theta_z$，正弦值、余弦值分别为$s_x, c_x, s_y, c_y, s_z, c_z$那么旋转矩阵为：

$$R(\theta_x,\theta_y,\theta_z)=R_z(\theta_z)R_y(\theta_y)R_x(\theta_x) = \left[ \begin{matrix} c_y c_z & c_z s_x s_y - c_x s_z & s_x s_z + c_x c_z s_y\\ c_y s_z & c_x c_z + s_x s_y s_z & c_x s_y s_z - c_z s_z\\ -s_y & c_y s_x & c_x c_y \end{matrix} \right]$$

2.2.2 由旋转矩阵求欧拉角

$$R = \left[ \begin{matrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{matrix} \right] = \left[ \begin{matrix} c_y c_z & c_z s_x s_y - c_x s_z & s_x s_z + c_x c_z s_y\\ c_y s_z & c_x c_z + s_x s_y s_z & c_x s_y s_z - c_z s_z\\ -s_y & c_y s_x & c_x c_y \end{matrix} \right]$$

解方程可得：

$$\theta_x = atan2(r_{32}, r_{33})$$

$$\theta_y = atan2(-r_{31}, \sqrt{r_{32}^2+r_{33}^2})$$

$$\theta_z = atan2(r_{21}, r_{11})$$

注：atan2()为C++中的函数，atan2(y，x) 求的是y/x的反正切，其返回值为[-pi,+pi]之间的一个数。

2.3 四元数

四元数（Quaternions）是由爱尔兰数学家哈密顿（William Rowan Hamilton）在1843年提出。

三维空间的任意旋转，都可以用绕三维空间的某个轴旋转过某个角度来表示，即所谓的Axis-Angle表示方法。这种表示方法里，Axis可用一个三维向量$(x,y,z)$来表示，$\theta$可以用一个角度值来表示，直观来讲，一个四维向量$(\theta,x,y,z)$就可以表示出三维空间任意的旋转。注意，这里的三维向量$(x,y,z)$只是用来表示axis的方向朝向，因此更紧凑的表示方式是用一个单位向量来表示方向axis，而用该三维向量的长度来表示角度值$\theta$。这样以来，可以用一个三维向量$(\theta*x, \theta*y, \theta*z)$就可以表示出三维空间任意的旋转，前提是其中$(x,y,z)$是单位向量。这就是旋转向量(Rotation Vector)的表示方式，OpenCV里大量使用的就是这种表示方法来表示旋转(见OpenCV相机标定部分的rvec)。

• 单位向量$(x,y,z)$旋转$\theta$角度后的四元数：

  $$(cos \frac{\theta}{2}, x*sin \frac{\theta}{2}, y*sin \frac{\theta}{2}, z*sin \frac{\theta}{2})$$

• 对于三维坐标的旋转，可以通过四元数乘法直接操作，与旋转矩阵操作可以等价，但是表示方式更加紧凑，计算量也可以小一些。

2.3.1 四元数基本概念

• 四元数的复数定义：

  $$\mathbf{q} = q_0 + q_1 i + q_2 j + q_3 k = [s, \mathbf{v}]$$

  • 其中 $q_0,q_1,q_2,q_3$均为实数, $s=q_0,\mathbf{v}=[q_1, q_2, q_3]$，$i^2=j^2=k^2=-1$
  • 对于 $i,j,k$ 本身的几何意义可以理解为一种旋转，其中 $i$ 代表 $x$ 轴与 $y$ 轴相交平面中 $x$ 轴正向向 $y$ 轴正向的旋转， $j$ 旋转代表 $z$ 轴与 $x$ 轴相交平面中 $z$ 轴正向向 $x$ 轴正向的旋转， $k$ 旋转代表 $y$ 轴与 $z$ 轴相交平面中 $y$ 轴正向向 $z$ 轴正向的旋转， $-i,-j,-k$ 分别代表 $i,j,k$ 的反向旋转。

• 四元数的模

  $$|q|=\sqrt{q_0^2 + q_1^2 + q_2^2 +q_3^2}$$

• 四元数的优点：

  • 非奇异表达（和欧拉角之类的表示相比）
  • 比矩阵更紧凑（更快速）
  • 单位四元数的对可以表示四维空间中的一个旋转

• 四元数与群

  所有单位四元数的集合组成一个三维球S3和在乘法下的一个群（李群）。S3是行列式为1的实正交3x3正交矩阵的群SO(3,R)的双面覆盖，因为每两个单位四元数通过上述关系对应于一个转动。群S3和SU(2)同构，SU(2)是行列式为1的复酉2x2矩阵的群。

  设$A=\{\mathbf{q}=q_0 + q_1 i + q_2 j + q_3 k | q_0,q_1,q_2,q_3 均为实数\}$，则$A$是一个环，并且是一个格，$A$中存在24个四元数，而它们是施莱夫利符号为$\{3,4,3\}$的正二十四胞体的顶点。

• 四元数的运算：

  $$\mathbf{p}_1 = [s_1, \mathbf{v}_1]=\begin{pmatrix} a_1 & b_1 & c_1 & d_1 \end{pmatrix}^T$$

  $$\mathbf{p}_2 = [s_2, \mathbf{v}_2]=\begin{pmatrix} a_2 & b_2 & c_2 & d_2 \end{pmatrix}^T$$

  • 四元数的加法

  $$\mathbf{p}_1 + \mathbf{p}_2 = s_1 + s_2 + \mathbf{v_1} + \mathbf{v_2} \\= (a_1 + a_2) + (b_1 + b_2)i + (c_1 + c_2)j + (d_1 + d_2)k$$

  • 四元数的乘法

  $$\mathbf{p}_1 \mathbf{p}_2 =s_1s_2 - \mathbf{v_1 v_2} + s_1 \mathbf{v_2} + s_2 \mathbf{v_1} + \mathbf{v_1 \times v_2}$$
  $$\mathbf{p}_1 \mathbf{p}_2 = \begin{pmatrix} a_1 a_2 - b_1 b_2 - c_1 c_2 - d_1 d_2 \\ a_1 b_2 + b_1 a_2 + c_1 d_2 - d_1 c_2 \\ a_1 c_2 - b_1 d_2 + c_1 a_2 + d_1 b_2 \\ a_1 d_2 + b_1 c_2 - c_1 b_2 + d_1 a_2 \end{pmatrix}$$

  注：四元数不满足交换律，故 $\mathbf{p}_1 \mathbf{p}_2 \neq \mathbf{p}_2 \mathbf{p}_1$，四元数的乘法不等同于外积。

  • 四元数的点积（内积）
    点积也叫欧几里得内积，四元数的点积等同于一个四维向量的点积。点积的值是$\mathbf{p_1} , \mathbf{p_2}$中相应元素的数值的乘积的和。

  $$\mathbf{p_1} \cdot \mathbf{p_2} = s_1 s_2 + \mathbf{v_1} \cdot \mathbf{v_2} = a_1 a_2 + b_1 b_2 + c_1 c_2 + d_1 d_2$$

  • 四元数的外积：$Outer(\mathbf{p_1,p_2})$

  • 四元数的偶积：$Even(\mathbf{p_1,p_2})$

  • 四元数的叉积：$\mathbf{p_1} \times \mathbf{p_2}$

  $$\mathbf{p_1} \times \mathbf{p_2} = \frac{\mathbf{p_1p_2} - \mathbf{p_2p_2}}{2}$$

  $$\mathbf{p_1} \times \mathbf{p_2} = \mathbf{v_1} \times \mathbf{v_2}$$

  $$\mathbf{p_1} \times \mathbf{p_2} = (c_1d_2-c_2d_1)i + (b_1d_2 - b_2d_1)j + (b_1c_2 - b_2c_1)k$$

  • 四元数的共轭 $\mathbf{q}^*$

  $$\mathbf{q}^* = s - \mathbf{v} = [s, -\mathbf{v}]$$

  $$\mathbf{q} \mathbf{q}^* = q_0^2 + q_1^2 + q_2^2 + q_3^2$$

  • 四元数的逆 $\mathbf{q}^{-1}$

  $$\mathbf{q}\mathbf{q}^{-1}=\mathbf{q}^{-1}\mathbf{q}=1$$

  $$\mathbf{q}^{-1} = \frac{\mathbf{q}^*}{||\mathbf{q}||^2}$$

  • 单位四元数
    单位四元数的共轭和逆相等 $\mathbf{q}^{-1}=\mathbf{q}^*$

• 四元数乘法的性质：

  1、满足结合律
  2、不满足交换律
  3、乘积的模等于模的乘积
  4、乘积的逆等于各个四元数的逆以相反的顺序相乘

2.3.2 四元数求旋转矩阵

• 方法1：

  • 已知四元数
    

    $$\mathbf{q} = q_0 + q_1 i + q_2 j + q_3 k = [s, \mathbf{v}]$$

  • 利用Rodrigues公式可以由四元数求得旋转矩阵$R$:
    

    $$R = \left[ \begin{matrix} 1 - 2 q_2^2 - 2 q_3^2 & 2q_1 q_2 - 2q_0 q_3 & 2 q_1 q_3 + 2 q_0 q_2 \\ 2q_1 q_2 + 2q_0 q_3 & 1 - 2 q_1^2 - 2 q_3^2 & 2 q_2 q_3 - 2 q_0 q_1 \\ 2 q_1 q_3 - 2 q_0 q_2 & 2 q_2 q_3 + 2 q_0 q_1 & 1 - 2 q_1^2 - 2 q_2^2 \end{matrix} \right ]$$

• 方法2：

• 亦可以将四元数转化为轴角 $\theta$ 与向量 $(x, y, z)$，然后再计算旋转矩阵（这样需要多计算一个arccos，不划算）
  

  $$\mathbf{q} = \begin{pmatrix} \theta & x & y & z \end{pmatrix}^T$$

• 利用Rodrigues公式可以由单位向量$\mathbf{\omega} = (x,y,z)$旋转$\theta$角度后的四元数求得旋转矩阵$R$:

$$R = e^{\mathbf{\omega} \theta} = I + \mathbf{\omega}_{\times} sin\theta + \mathbf{\omega}_{\times}^2 (1 - cos\theta) \\ = I + \left[ \begin{matrix} 0 & -z & y\\ z & 0 & -x \\ -y & x & 0 \end{matrix} \right ] sin\theta + \left[ \begin{matrix} -y^2-z^2 & xy & xz\\ xy & -x^2-z^2 & yz \\ xz & yz & -x^2-y^2 \end{matrix} \right ] (1-cos\theta)\\ = \left[ \begin{matrix} 1 & -zsin\theta & ysin\theta\\ zsin\theta & 1 & -xsin\theta \\ -ysin\theta & xsin\theta & 1 \end{matrix} \right ] + \left[ \begin{matrix} -y^2-z^2 & xy & xz\\ xy & -x^2-z^2 & yz \\ xz & yz & -x^2-y^2 \end{matrix} \right ] (1-cos\theta)\\ = \left[ \begin{matrix} 1-(y^2+z^2)(1-cos\theta) & -zsin\theta + xy(1-cos\theta) & ysin\theta + xz(1-cos\theta) \\ zsin\theta + xy(1-cos\theta) & 1 - (x^2+z^2)(1-cos\theta) & -xsin\theta + yz(1-cos\theta) \\ -ysin\theta + xz(1-cos\theta) & xsin\theta + yz(1-cos\theta) & 1-(x^2+y^2)(1-cos\theta) \end{matrix} \right ] \\ = \left[ \begin{matrix} cos\theta+x^2(1-cos\theta) & -zsin\theta + xy(1-cos\theta) & ysin\theta + xz(1-cos\theta) \\ zsin\theta + xy(1-cos\theta) & cos\theta+y^2(1-cos\theta) & -xsin\theta + yz(1-cos\theta) \\ -ysin\theta + xz(1-cos\theta) & xsin\theta + yz(1-cos\theta) & cos\theta+ z^2(1-cos\theta) \end{matrix} \right ]$$

$$R = \left[ \begin{matrix} cos\theta+x^2(1-cos\theta) & -zsin\theta + xy(1-cos\theta) & ysin\theta + xz(1-cos\theta) \\ zsin\theta + xy(1-cos\theta) & cos\theta+y^2(1-cos\theta) & -xsin\theta + yz(1-cos\theta) \\ -ysin\theta + xz(1-cos\theta) & xsin\theta + yz(1-cos\theta) & cos\theta+ z^2(1-cos\theta) \end{matrix} \right ]$$

2.3.3 旋转矩阵求四元数

• 情况1：

  $$q_0 = \frac{\sqrt{1+r_{11}+r_{22}+r_{33}}}{2}$$

  $$q_1 = \frac{r_{32}-r_{23}}{4q_0}$$

  $$q_2 = \frac{r_{13}-r_{31}}{4q_0}$$

  $$q_3 = \frac{r_{21}-r_{12}}{4q_0}$$

  其中要满足 $q_0 \neq 0$，$1+r_{11}+r_{22}+r_{33}>0$，即 $1+tr(R)>0$

• 情况2：
  如果$q_0$趋近于0，$tr(R)$趋近于-1,则求解四元数的过程为：

  • 2.1 如果$max\{r_{11},r_{22},r_{33}\}=r_{11}$

    $$t = \sqrt{1+r_11 - r_{22} - r_{33}}$$

    $$q_0 = \frac{r_{32} - r_{23}}{t}$$

    $$q_1 = t/4$$

    $$q_2 = \frac{r_{13} + r_{31}}{t}$$

    $$q_3 = \frac{r_{12} + r_{21}}{t}$$

  • 2.2 如果$max\{r_{11},r_{22},r_{33}\}=r_{22}$

    $$t = \sqrt{1 - r_11 + r_{22} - r_{33}}$$

    $$q_0 = \frac{r_{13} - r_{31}}{t}$$

    $$q_1 = \frac{r_{12} + r_{21}}{t}$$

    $$q_2 = t/4$$

    $$q_3 = \frac{r_{32} + r_{23}}{t}$$

  • 2.3 如果$max\{r_{11},r_{22},r_{33}\}=r_{33}$

    $$t = \sqrt{1 - r_11 - r_{22} + r_{33}}$$

    $$q_0 = \frac{r_{21} - r_{12}}{t}$$

    $$q_1 = \frac{r_{13} + r_{31}}{t}$$

    $$q_2 = \frac{r_{23} - r_{32}}{t}$$

    $$q_3 = t/4$$

参考资料

• 相关文章

  • 机器学习、深度学习、计算机视觉、自然语言处理及应用案例——干货分享（持续更新……）
  • 相机标定（Camera calibration）原理、步骤

• 1、三维旋转：旋转矩阵，欧拉角，四元数

• 2、欧拉角、四元数和旋转矩阵

• 3、欧拉角和旋转矩阵的转换

• 4、三维空间中的旋转：旋转矩阵、欧拉角

• 5、旋转矩阵、欧拉角、四元数比较

• 6、刚体在三维空间的旋转(关于旋转矩阵、DCM、旋转向量、四元数、欧拉角)

• 7、3D计算机图形学-变换矩阵、欧拉角、四元数

• 8、欧拉角

• 9、四元数

• 10、【泡泡机器人SLAM原创专栏-四元数运动学】一：四元数和旋转

• 11、3D图形:矩阵、欧拉角、四元数与方位的故事