欧拉法求解微分方程_欧拉法解微分方程-程序员宅基地
文章目录
欧拉法是一种求解微分方程的数值方法。微分方程的目标是求出方程的具体表达式,但数值方法则是根据方程求出其每一个点,而不是找出表达式,在工程上具有很大的实用性。
欧拉法求解微分方程组的原理
设有微分方程:
d x ( t ) d t = f ( x ) \frac{dx(t)}{dt} = f(x) dtdx(t)=f(x)
x ( t 0 ) = x 0 x(t_0)=x_0 x(t0)=x0已知。
我们对上述方程进行积分,积分区域为 [ t 0 , t 1 ] , Δ t = t 1 − t 0 [t_0,t_1],\Delta t = t_1-t_0 [t0,t1],Δt=t1−t0,可得:
x ( t 1 ) = x ( t 0 ) + ∫ t 0 t 1 f ( t ) d t x(t_1)=x(t_0)+\int_{t_0}^{t_1}f(t)dt x(t1)=x(t0)+∫t0t1f(t)dt
其中 x ( t 1 ) x(t_1) x(t1)就是我们要求解的东西了。于是,就差积分怎么解决了。
对于欧拉法来说,积分是靠梯形面积来近似,如下所示:
∫ t 0 t 1 f ( t ) d t = f ( x ( t 0 ) ) ( t 1 − t 0 ) = f ( x 0 ) Δ t \int_{t_0}^{t_1}f(t)dt = f(x(t_0))(t_1-t_0)=f(x_0)\Delta t ∫t0t1f(t)dt=f(x(t0))(t1−t0)=f(x0)Δt
带入上述方程即可得:
x ( t 1 ) = x ( t 0 ) + f ( x 0 ) Δ t x(t_1)=x(t_0)+f(x_0)\Delta t x(t1)=x(t0)+f(x0)Δt
按照上式进行递推,即可得:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
其中 x 0 x_0 x0 已知。问题就搞定了。
*欧拉法原理图解
因为
f ( x k ) = d x d t ∣ t = t k f(x_k) = \frac{dx}{dt}|_{t=t_k} f(xk)=dtdx∣t=tk
所以递推式可以写成:
x k + 1 = x k + d x d t ∣ t = t k Δ t x_{k+1} = x_{k} + \frac{dx}{dt}|_{t=t_k}\Delta t xk+1=xk+dtdx∣t=tkΔt
而 d x d t \frac{dx}{dt} dtdx是所求方程 x ( t ) x(t) x(t)的斜率,因此实际上是将下图的阴影部分的面积来替代积分表达式:

欧拉法数值稳定性讨论
方便讨论,我们取一种简单情况,设有微分方程:
d x ( t ) d t = a x \frac{dx(t)}{dt} = ax dtdx(t)=ax
什么是数值稳定性问题?
假设 k 步计算中, x k x_k xk与实际值存在误差 ρ k \rho_k ρk,则第 k+1 步计算中,误差是否会增大。若是,则不稳定啦。因为越往后计算,这个误差肯定是越爆炸的。
那么欧拉法数值稳定性如何呢?首先假设 x k x_k xk与实际值存在误差 ρ k \rho_k ρk,根据递推公式:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
设 f ( x k ) = a x k f(x_{k})=ax_{k} f(xk)=axk而:
x ^ k = x k + ρ k \hat{x}_k = x_k + \rho_{k} x^k=xk+ρk
故第 k+1 步时时:
x ^ k = ( 1 + a Δ t ) ( x k + ρ k ) = x k + 1 + ( 1 + a Δ t ) ρ k \hat{x}_k = (1+a\Delta t)(x_k+\rho_k)=x_{k+1}+(1+a\Delta t)\rho_k x^k=(1+aΔt)(xk+ρk)=xk+1+(1+aΔt)ρk
于是 k+1 步的误差为:
ρ k + 1 = ( 1 + a Δ t ) ρ k \rho_{k+1} = (1+a\Delta t)\rho_k ρk+1=(1+aΔt)ρk
若要求稳定,则必须有 ∣ 1 + a Δ t ∣ ≤ 1 |1+a\Delta t| \leq 1 ∣1+aΔt∣≤1
于是可得欧拉法的数值稳定区域如下:

欧拉法误差分析——局部截断误差
微分方程 d x d t = f ( x ) \frac{dx}{dt} = f(x) dtdx=f(x),用欧拉法时,我们的迭代方程是:
x k = x k − 1 + f ( x k − 1 ) Δ t = x k − 1 + d x d t ∣ t k − 1 Δ t x_{k} = x_{k-1} + f(x_{k-1})\Delta t =x_{k-1} + \frac{dx}{dt}|_{t_{k-1}}\Delta t xk=xk−1+f(xk−1)Δt=xk−1+dtdx∣tk−1Δt。
若对 x k x_{k} xk 进行泰勒展开,可得:
x ( t k ) = x ( t k − 1 + Δ t ) = x k − 1 + x ′ ( t k − 1 Δ t + x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x(t_{k}) = x(t_{k-1}+\Delta t) = x_{k-1} + x^{\prime}(t_{k-1} \Delta t + x^{\prime\prime}(t_{k-1}) \Delta t^2 + \cdots x(tk)=x(tk−1+Δt)=xk−1+x′(tk−1Δt+x′′(tk−1)Δt2+⋯
因此,欧拉法的截断误差为:
x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x^{\prime\prime}(t_{k-1}) \Delta t^2+ \cdots x′′(tk−1)Δt2+⋯
由于有 Δ t 2 \Delta t^2 Δt2,所以我称欧拉法的精度为 2-1 = 1 阶。
改进欧拉法原理
欧拉法是用梯形的面积来近似积分的,而且梯形的上底是用 KaTeX parse error: Expected 'EOF', got '}' at position 7: x_[i-1}̲时,曲线 x ( t ) x(t) x(t)的斜率来近似计算的,所以不太好,可以看到的是,欧拉法的精度只有一阶,其阶段误差与 Δ t 2 \Delta t^2 Δt2有关。这个误差之所以那么大,是因为我们在求积分(面积)的时候,用了以 x k − 1 x_{k-1} xk−1为上底的梯形去近似他。因此,我们需要对这个梯形的上底进行一定的修正。
首先,根据递推公式求出:
x k ( 0 ) = x k − 1 + f ( x k − 1 ) Δ t x_{k}^{(0)} = x_{k-1} + f(x_{k-1}) \Delta t xk(0)=xk−1+f(xk−1)Δt
之后再求出修正后的 x k x_{k} xk:
x k = x k − 1 + 1 2 ( f ( x k − 1 + x k ( 0 ) ) Δ t x_k = x_{k-1}+\frac{1}{2}(f(x_{k-1}+x_{k}^{(0)})\Delta t xk=xk−1+21(f(xk−1+xk(0))Δt
其原理图如下:
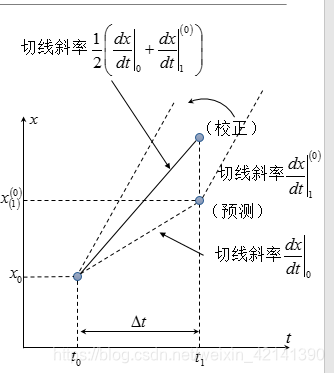
改进欧拉法的稳定性分析
设微分方程为 d x d t = λ x \frac{dx}{dt} = \lambda x dtdx=λx,于是KaTeX parse error: Undefined control sequence: \ambda at position 16: x_{k}^{(0)]=(1+\̲a̲m̲b̲d̲a̲\Delta t)x_{k-1…, f ( x k ( 0 ) = λ ( 1 + λ Δ t ) x k − 1 f(x_{k}^{(0)}=\lambda(1+\lambda\Delta t)x_{k-1} f(xk(0)=λ(1+λΔt)xk−1,于是 x k = ( 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ) x k − 1 x_{k} = (1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2)x_{k-1} xk=(1+λΔt+21(λΔt)2)xk−1
所以误差不增值的条件为: ∣ 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ∣ ≤ 1 |1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2|\leq1 ∣1+λΔt+21(λΔt)2∣≤1,表现在图上,即为:
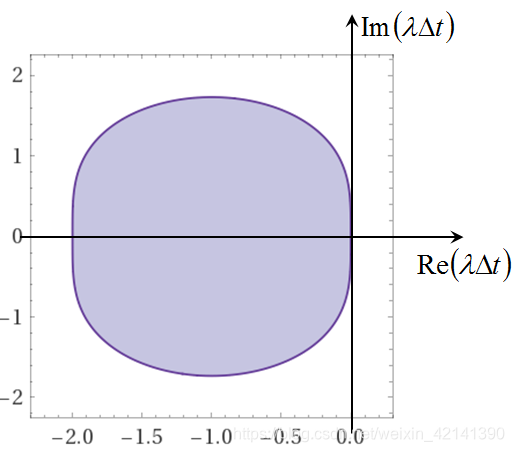
对比欧拉法,显然稳定区域大了一点。
改进欧拉法的误差分析
因为 f ( x k 0 ) = d x d t ∣ x k − 1 + d 2 x d t 2 ∣ x k − 1 Δ t 2 + O ( Δ t 2 ) f(x_{k}^{0}) = \frac{dx}{dt}|_{x_{k-1}}+\frac{d^{2}x}{dt^2}|_{x_{k-1}}\Delta t^2+O(\Delta t^2) f(xk0)=dtdx∣xk−1+dt2d2x∣xk−1Δt2+O(Δt2)
于是 x k = x k − 1 + d x d t ∣ x k − 1 Δ t + d 2 x d t 2 ∣ x k − 1 Δ t 2 x_{k} = x_{k-1}+\frac{dx}{dt}|_{x_{k-1}}\Delta t+\frac{d^2x}{dt^2}|_{x_{k-1}}\Delta t^2 xk=xk−1+dtdx∣xk−1Δt+dt2d2x∣xk−1Δt2
对比泰勒展开,可知其误差为 O ( Δ t 3 ) O(\Delta t^3) O(Δt3),因此精确度为 3-1 = 2阶!
隐式梯形法
隐式梯形法也是利用 x k x_k xk 来改善上底,只是其递推公式为:
x k = x k − 1 + Δ t 2 ( f ( x k − 1 ) + f ( x k ) ) x_{k} = x_{k-1} + \frac{\Delta t}{2}(f(x_{k-1})+f(x_{k})) xk=xk−1+2Δt(f(xk−1)+f(xk))
因此,上底的修正,包含在上述方程中。因此,不同于欧拉法,每一次迭代,隐式梯形法都要求解一次代数方程。
隐式梯形法的稳定性和误差
首先是稳定性,同样对于微分方程 d x d t = λ x \frac{dx}{dt}=\lambda x dtdx=λx,可得其误差的表达式为:
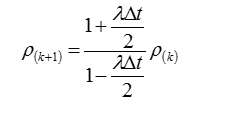
误差不增值条件: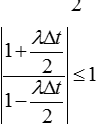
整理可得: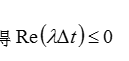
因此其稳定区域为:复平面的左半部分,可见比改进欧拉发、欧拉法要大得多!!
至于误差,同样可以证明的是隐式梯形法的精确度为2阶。
案例
可见求解区域为 [0,1],我们设置求解的步数为 100,也即 Δ t = 0.01 s \Delta t = 0.01s Δt=0.01s,代码如下:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -20*x
def uler(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = x[i]+f(x[i])*dt
x.append(xk)
return x,t
def uler2(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xkk = x[i]+f(x[i])*dt
xk = x[i]+ 1/2*(f(x[i])+f(xkk))*dt
x.append(xk)
return x,t
import sympy
x = sympy.symbols('x')
def uler3(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = (x[i]+dt*f(x[i])/2)/(1+10*dt)
x.append(xk)
return x,t
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
font1 = {
'family' : 'SimHei',
'weight' : 'normal',
'size' : 15,
}
def myplot(n,x0,t0,tn,f):
x1,t = uler(n,x0,t0,tn,f)
x2,t = uler2(n,x0,t0,tn,f)
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.plot(t,x1,linewidth=3,color='r',label='欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
plt.subplot(1,3,2)
plt.plot(t,x2,linewidth=3,color='b',label='改进欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
x3,t = uler3(n,x0,t0,tn,f)
plt.subplot(1,3,3)
plt.plot(t,x3,linewidth=3,color='g',label='隐式梯形法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
if __name__ == '__main__':
myplot(100,1,0,1,f)
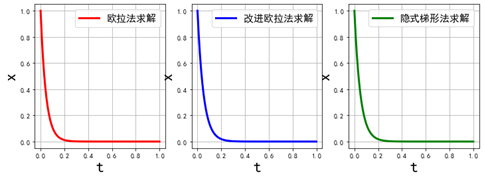
求解结果:
可以修改步长为 15,可得:
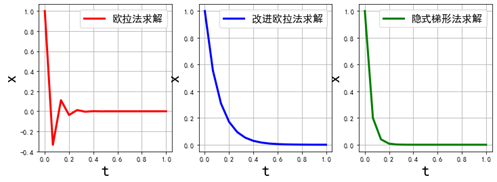
为什么步数为 15,结果就变形了呢?这是因为算法的稳定性、误差的原因,这里不再分析。
智能推荐
oracle 12c 集群安装后的检查_12c查看crs状态-程序员宅基地
文章浏览阅读1.6k次。安装配置gi、安装数据库软件、dbca建库见下:http://blog.csdn.net/kadwf123/article/details/784299611、检查集群节点及状态:[root@rac2 ~]# olsnodes -srac1 Activerac2 Activerac3 Activerac4 Active[root@rac2 ~]_12c查看crs状态
解决jupyter notebook无法找到虚拟环境的问题_jupyter没有pytorch环境-程序员宅基地
文章浏览阅读1.3w次,点赞45次,收藏99次。我个人用的是anaconda3的一个python集成环境,自带jupyter notebook,但在我打开jupyter notebook界面后,却找不到对应的虚拟环境,原来是jupyter notebook只是通用于下载anaconda时自带的环境,其他环境要想使用必须手动下载一些库:1.首先进入到自己创建的虚拟环境(pytorch是虚拟环境的名字)activate pytorch2.在该环境下下载这个库conda install ipykernelconda install nb__jupyter没有pytorch环境
国内安装scoop的保姆教程_scoop-cn-程序员宅基地
文章浏览阅读5.2k次,点赞19次,收藏28次。选择scoop纯属意外,也是无奈,因为电脑用户被锁了管理员权限,所有exe安装程序都无法安装,只可以用绿色软件,最后被我发现scoop,省去了到处下载XXX绿色版的烦恼,当然scoop里需要管理员权限的软件也跟我无缘了(譬如everything)。推荐添加dorado这个bucket镜像,里面很多中文软件,但是部分国外的软件下载地址在github,可能无法下载。以上两个是官方bucket的国内镜像,所有软件建议优先从这里下载。上面可以看到很多bucket以及软件数。如果官网登陆不了可以试一下以下方式。_scoop-cn
Element ui colorpicker在Vue中的使用_vue el-color-picker-程序员宅基地
文章浏览阅读4.5k次,点赞2次,收藏3次。首先要有一个color-picker组件 <el-color-picker v-model="headcolor"></el-color-picker>在data里面data() { return {headcolor: ’ #278add ’ //这里可以选择一个默认的颜色} }然后在你想要改变颜色的地方用v-bind绑定就好了,例如:这里的:sty..._vue el-color-picker
迅为iTOP-4412精英版之烧写内核移植后的镜像_exynos 4412 刷机-程序员宅基地
文章浏览阅读640次。基于芯片日益增长的问题,所以内核开发者们引入了新的方法,就是在内核中只保留函数,而数据则不包含,由用户(应用程序员)自己把数据按照规定的格式编写,并放在约定的地方,为了不占用过多的内存,还要求数据以根精简的方式编写。boot启动时,传参给内核,告诉内核设备树文件和kernel的位置,内核启动时根据地址去找到设备树文件,再利用专用的编译器去反编译dtb文件,将dtb还原成数据结构,以供驱动的函数去调用。firmware是三星的一个固件的设备信息,因为找不到固件,所以内核启动不成功。_exynos 4412 刷机
Linux系统配置jdk_linux配置jdk-程序员宅基地
文章浏览阅读2w次,点赞24次,收藏42次。Linux系统配置jdkLinux学习教程,Linux入门教程(超详细)_linux配置jdk
随便推点
matlab(4):特殊符号的输入_matlab微米怎么输入-程序员宅基地
文章浏览阅读3.3k次,点赞5次,收藏19次。xlabel('\delta');ylabel('AUC');具体符号的对照表参照下图:_matlab微米怎么输入
C语言程序设计-文件(打开与关闭、顺序、二进制读写)-程序员宅基地
文章浏览阅读119次。顺序读写指的是按照文件中数据的顺序进行读取或写入。对于文本文件,可以使用fgets、fputs、fscanf、fprintf等函数进行顺序读写。在C语言中,对文件的操作通常涉及文件的打开、读写以及关闭。文件的打开使用fopen函数,而关闭则使用fclose函数。在C语言中,可以使用fread和fwrite函数进行二进制读写。 Biaoge 于2024-03-09 23:51发布 阅读量:7 ️文章类型:【 C语言程序设计 】在C语言中,用于打开文件的函数是____,用于关闭文件的函数是____。
Touchdesigner自学笔记之三_touchdesigner怎么让一个模型跟着鼠标移动-程序员宅基地
文章浏览阅读3.4k次,点赞2次,收藏13次。跟随鼠标移动的粒子以grid(SOP)为partical(SOP)的资源模板,调整后连接【Geo组合+point spirit(MAT)】,在连接【feedback组合】适当调整。影响粒子动态的节点【metaball(SOP)+force(SOP)】添加mouse in(CHOP)鼠标位置到metaball的坐标,实现鼠标影响。..._touchdesigner怎么让一个模型跟着鼠标移动
【附源码】基于java的校园停车场管理系统的设计与实现61m0e9计算机毕设SSM_基于java技术的停车场管理系统实现与设计-程序员宅基地
文章浏览阅读178次。项目运行环境配置:Jdk1.8 + Tomcat7.0 + Mysql + HBuilderX(Webstorm也行)+ Eclispe(IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持)。项目技术:Springboot + mybatis + Maven +mysql5.7或8.0+html+css+js等等组成,B/S模式 + Maven管理等等。环境需要1.运行环境:最好是java jdk 1.8,我们在这个平台上运行的。其他版本理论上也可以。_基于java技术的停车场管理系统实现与设计
Android系统播放器MediaPlayer源码分析_android多媒体播放源码分析 时序图-程序员宅基地
文章浏览阅读3.5k次。前言对于MediaPlayer播放器的源码分析内容相对来说比较多,会从Java-&amp;gt;Jni-&amp;gt;C/C++慢慢分析,后面会慢慢更新。另外,博客只作为自己学习记录的一种方式,对于其他的不过多的评论。MediaPlayerDemopublic class MainActivity extends AppCompatActivity implements SurfaceHolder.Cal..._android多媒体播放源码分析 时序图
java 数据结构与算法 ——快速排序法-程序员宅基地
文章浏览阅读2.4k次,点赞41次,收藏13次。java 数据结构与算法 ——快速排序法_快速排序法